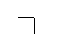
Axiom 1. The law of calling
The value of a call made again is the value of the call.
Axiom 2. The law of crossing
The value of a crossing made again is not the value of
the crossing.
These laws are expressed in many ways in the book. The idea is that we can make a mark to distinguish two states: the marked state and the unmarked state. This is usually done in the work by using a type of cross to mark or distinguish something.
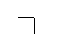
The two laws expressed in this form are:
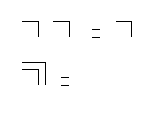
Now skipping ahead to the end of the book in APPENDIX 2
Interpretative theorem 1
If the primary algebra is interpreted so that integral expressions are true, and if each of a number of class-inclusion premisses is sententially transcribed in it, and if variables representing the same same sentance at odd and even levels are cancelled, what remains, when retranscribed, is the logical conclusion.
Four very interesting examples of are provided:
1. A dilemma from Maurant:
If we are to have a sound economy, we must not inflate the currency. But if we are to have an expanding economy, we must inflate the currency. Either we inflate the currency or we do not inflate the currency. Therefore, we shall have neither a sound economy nor an expanding economy.
2. A syllogism in Barbara, in the form of Whitehead and Russell's implicational logic:
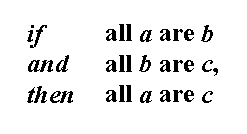
3. An equivalence problem from B V Bowden, Faster than Thought:
4. Lewis Carroll's last sorties:
These problems might appear difficult to someone who does
not consider themself to be a mathematician, and I suspect
that they might seem difficult to most programmers.
Certainly most programmers would consider that writing a
program that could solve these problems would be quite
difficult. But these are all trivial problems when then are
solved using the calculus of indications.
Example 1 can be reduced to:
Which is clearly not a dilemma.
we have an expanding economy
or we have a sound economy
Example 2 is shown to be true.
Example 3 can be reduced to:
This type of reduction of logical expression can be tremendous value in expert systems, or AI applications that appear to have a great deal of reasoning power.
A program to do this must perform several steps.
1. Parse strings of text to produce a transcription of the text into a representation in a computer compatible format as expresssed in the calculus of indications.
2. Process this representation with a reduction engine applying the basic laws of condensation and cancellation.
3. Re-transcribe the reduced expression back to english language strings.
Step three could just as easily compile the simplified expression into an expert system.
No Forth code will be presented in this preliminary description of the Forth Meets Laws of Form project. But I will show the computer compatible format for notation in the calculus of indications.
The graphic crosses that are used in the textbook are not suitable for representation in binary format, and I have chosen the underline character _ to represent a cross, and a number to represent the number of expressions to be crossed. In other words the expression cross is just _ , and ``if a then b'' becomes: ``a_1b''. More precisely it is a pointer to the string a, the token for a cross _ and the number representing the number of string tokens to be crossed, and a pointer to the string b.
This format provides the use of a general purpose logic reduction engine that can process data structures of this format on a computer as expressed above as step two. Step three becomes trival.
Step one needs to be able to parse ascii text and recognize certain English words. These words then delimit strings that are used in the transcribed expressions. This will be approached by implementing a small set of words to handle particular examples, and later expanded with more recognizable English expressions to control parsing.
The details of the Forth programs to implement these three steps will be presented in further reports on the project, if this paper can suggest some understanding of the idea behind the project.